
Hőtani szempontból az öntvényekkel kapcsolatban két alapvető kihívást kell kezelnünk. Az első, hogy az öntvény és a hozzá kapcsolódó fém kiegészítők, úgymint tápfej és beömlőrendszer tömegének megfelelő fémet meg kell olvasztani. A második, hogy az olvadt fém hőtartalmát el kell vezetni az öntvényből. Ebben a cikkben ez utóbbi területet vesszük szemügyre. Bemutatjuk, hogy az általunk használt öntvény hűtés CFD szimuláció hogyan teszi hatékonyabbá és olcsóbbá autóipari öntvények gyártását.
A számítógépes szimuláció segítségével tehát megtervezhető az öntvények hűtéstechnológiája. Ellenőrizhető, hogy az öntvény felhasználója által elvárt mechanikai paraméterek, amelyek alapvetően függenek a kokillából éppen csak kiemelt öntvény hűtésének sebességétől és módjától, teljesülnek-e a folyamat végén.
Az öntvény hűtés CFD szimuláció alkalmazása lehetőséget ad arra is, hogy egy hűtősor még a megépítése előtt, amikor a konstrukció még csak számítógépes modell formájában létezik, ellenőrizhető legyen. A szimuláció egy olyan laboratóriumként működik, ahol szabadon kísérletezhetünk. Kipróbálhatunk új hűtősor konfigurációkat, levegős vagy vizes hűtést, légáramba kevert vízpermet alkalmazását. Vagy egyszerűen csak az öntvény és a hűtőlevegő fúvóka egymáshoz viszonyított pozíciójának különböző verzióit.


Az öntvény hőtartalma vs. az elszállított hőmennyiség
Ahhoz, hogy egy hűtősort ellenőrizzünk, vagy meghatározzuk azt az intenzitást, amellyel az öntvényt adott idő alatt le kell hűtenünk például 530°C-ról 80°C-ra, tudunk kell, hogy a folyamat elején mekkora az öntvény hőtartalma.
Tekintsünk a teljes folyamatra úgy, mint egy mérleg két serpenyőjére. Az egyik oldalon a kokillából már kiemelt, tehát külső felületein megszilárdult öntvény hűtési folyamat elején érvényes hőtartalma, míg a másik serpenyőben – levegős hűtés esetén – a vizsgált öntvény és hűtőlevegő fúvóka egymáshoz viszonyított pozíciója, a hűtőlevegő sebessége, hőmérséklete, páratartalma, azaz a hűtés intenzitása, tehát az elvonható hőmennyiség található.
A két oldalt egy-egy képlet jellemzi, ezek a következők:
az öntvény hőtartalma Joule-ban: Q=c∙m∙ΔT, (1)
az elvont hőteljesítmény Wattban: Pq=α∙F(Tfal-Tlev). (2)
ahol:
c: fajhő [J/kgK],
ΔT: a hőközlés során az m tömegű test hőmérséklet növekedése [°C],
α: hőátadási tényező [W/m2K],
F: a hőelvonásban résztvevő felület nagysága [m2],
Tfal: a hűtendő felület hőmérséklete [°C]
Tlev: a hűtésre felhasznált közeg, jelen esetben levegő hőmérséklete [°C]
A két oldal között a hűtés megvalósítására előírt idő teremti meg a kapcsolatot, mivel W=J/s.
Az öntvény hőtartalma
Vegyük szemügyre először az öntvény hőtartalmát. Itt abból a hőmennyiségből indulunk ki, amelyet az öntvény összeállítás fém és homok tömege a hűtősorra kerülés pillanatában tartalmaz. Ha ismert az öntvény és homokmagok átlaghőmérséklete, vagy mérések és öntészeti szimulációk eredményeként a felületi és belső hőmérséklet eloszlása, ha ismert a fém és homok tömege, illetve a fém és homok fajhője, akkor az (1) képlet szerint kiszámolható a hűtősorra kerülő öntvény összeállítás hőtartalma. A példa kedvéért egy 33.2 kg fémet tartalmazó öntvény összeállítás esetén, ha 530°c-ról 80°C-ra kell hűtenünk, ez az érték 18MJ.
Megjegyezzük, hogy az öntvény hőtartalmának meghatározásakor kiindulhatunk a 33,2 kg fém megolvasztásához szükséges hőmennyiségből is. A számítás során figyelembe kell venni a fém pl. 30°C-ról 700°C-ra történő hevítésének energiaigényét (szintén az (1) képlettel számítható) és ehhez hozzá kell adnunk a szilárd fázisból olvadék fázisba történő átalakuláshoz szükséges látens hő mértékét.
Az így kiszámított hőtartalommal bíró olvadék kerül a kokillába, ahol ez a hőmennyiség a kokilla hűtése miatt és az olvadék fázisból szilárd fázisba történő átalakulás révén csökken, illetve egy része a fémből hővezetéssel a homokmagokba kerül. Ez az igen komplex hőmérséklet eloszlású, többféle hővezetési tényezőjű és fajhőjű anyagból álló öntvény összeállítás kerül a hűtősor elejére.
Mivel a hűtősoron végighaladó öntvény összeállítás tartalmazza a homokmagokat is, az ezekben felhalmozott hőt is a soron bevezetett hűtőlevegőnek kell elszállítania. Bizonyos konstrukcióknál előfordul, hogy az öntvény külső részén lévő magjelek leesnek, mert a mag az öntvény kontúrján kívül teljesen átég. Ennek hőtani szempontból kedvező hatása abban testesül meg, hogy a leesett homokdarab vitte magával a saját hőtartalmát is, amit így nem kell a soron tovább hűteni.
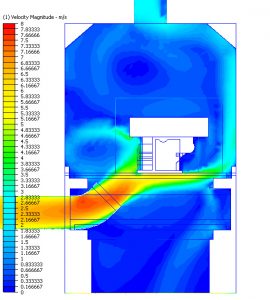
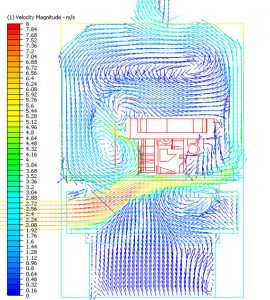
Tehát ha a fenti példát visszük tovább, akkor az öntvény összeállítás azon hőtartalma, amelyet a hűtősoron kell elvonnunk 18 MJ. Ezzel a 18 MJ-lal áll szemben a hűtősor hőelvonási teljesítménye, amely teljesítményre ható, a (2) képletben szereplő tagokat a hűtősor üzemeltetője vagy tervezője kisebb-nagyobb mértékben befolyásolhatja.
Az elszállított hőmennyiség
Vegyük sorra, hogy milyen lehetőségeink vannak a hűtés intenzitásának növelésére. Ha a képletben szereplő hőmérsékleteket tekintjük az látszik, hogy a hűtési folyamat előre haladtával a hőmérsékletek befolyásoló ereje egyre kisebb, hiszen ahogy a fal hőmérséklete csökken, az állandónak tekinthető hűtőlevegő hőmérséklet mellett e kettő különbsége egyre kisebb, tehát a szorzatban egyre kisebb mértékben vesz részt.
A (2) képletben szereplő F felület állandó, némi esélyünk a növelésére akkor van, ha a fentebb említett okból kifolyólag az öntvény külsején lévő magok leesnek és ezzel fém felületeket tesznek elérhetővé a hűtőlevegő számára.
Marad tehát a (2) képletben szereplő hőátadási tényező (α), amelyet a technológiát tervező teljes mértékben befolyásolhat. Mitől függ ugyanis a hőátadási tényező értéke? Nos, elsősorban a hűtőlevegő sebességétől, de van hatása a hűtendő felület környezetében kialakuló áramlás jellegének, azaz hogy a hűtendő felületet támadó levegő milyen gyorsan képes a felületről felvett hővel onnan eltávozni, és a hűtőközeg anyagtulajdonságainak is van szerepe. A hőátadási tényezővel kapcsolatos legnagyobb kihívás abban áll, hogy értéke nehezen mérhető, ráadásul egy könnyűfém öntvény kontúrja nagyon bonyolult lehet, sok felületből állhat, amely felületeken az alfa nagy mértékben változhat. Viszont a technológia megtervezéséhez az alfa értékére mindenképpen szükség van.
A lényeg a hőátadási tényező nagysága
Az alábbi táblázat a különböző sebességgel áramoltatott közegek által elérhető α értékét tartalmazza tól-ig formátumban, tehát az adatok csak tájékoztató jellegűnek minősíthetők. A táblázatból látható, hogy hőtani szempontból a leghatékonyabb, ha a forró öntvényt vízzel teli kádba engedjük. De előfordulhat, hogy ebben az esetben nem teljesülnek az öntvénnyel szemben támasztott mechanikai tulajdonságokra, különösen a nyúlásra vonatkozó előírások. Meg kell tehát találnunk azt a módszert, amely a lehetőségeinken belül a leghatékonyabb hűtést biztosítja úgy, hogy közben az összes technológiai paraméter (pl. szakítószilárdság, nyúlás) folyamatbiztosan teljesül. Ehhez pedig a tervezés szakaszában pontosan kell tudnunk, hogy milyen hőátadási tényezővel számolhatunk.
Ezen a ponton kerül képbe az áramlás- és hőtechnikai (röviden CFD) szimuláció. Ebben a számítógép által létrehozott virtuális laboratóriumban ugyanis fel tudunk építeni olyan modelleket, amelyekben részletesen vizsgálhatjuk az öntvény és a hűtőlevegő kapcsolatát. Elemezhetjük a közelebb, vagy távolabb helyezett levegő fúvóka hatását. Kipróbálhatjuk, hogy az alfa mekkora mértékű növekedését okozza, ha a fúvókából kilépő levegő sebességét növeljük. De akár összehasonlíthatunk eltérő alakú fúvókákat is, sőt megnézhetjük a hűtőlevegő páratartalmának hatását az elvont hő mennyiségére vonatkozóan.
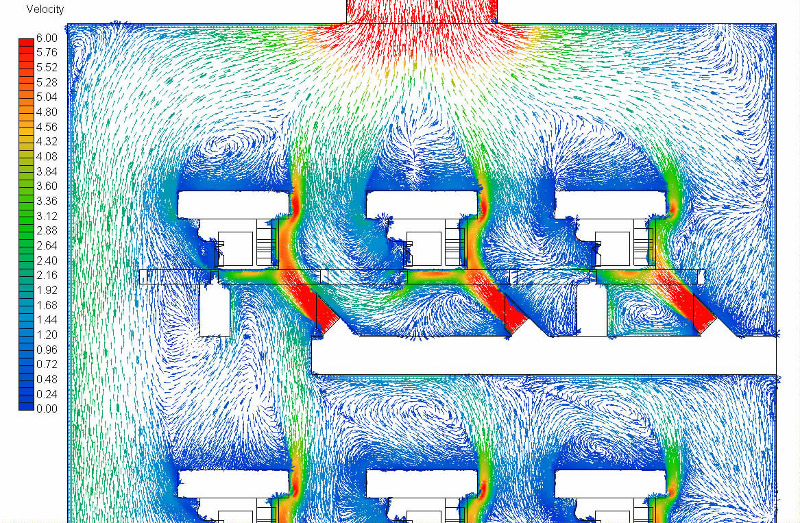
E modellek kiszámításának eredménye a tervezéshez nélkülözhetetlen alfa értéke és annak öntvény felületén történő eloszlása. Az öntvény hűtés CFD szimuláció módszere továbbá képes arra is, hogy meghatározza a felületről elvont hő mennyiségét W/m2-ben, azaz a (2) képlettel keresett eredményt.
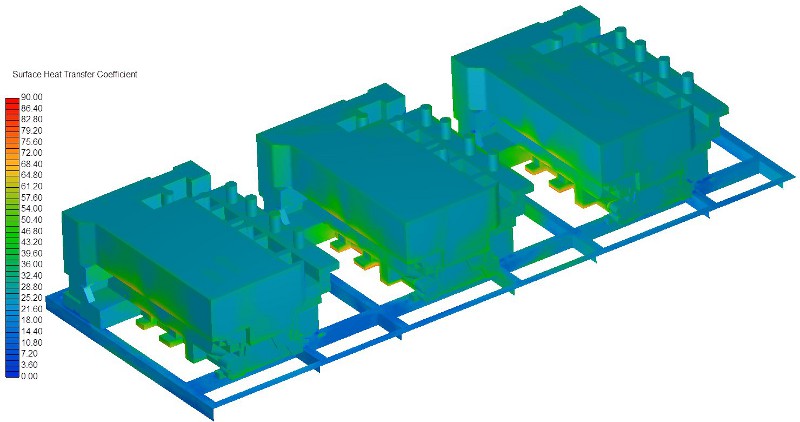
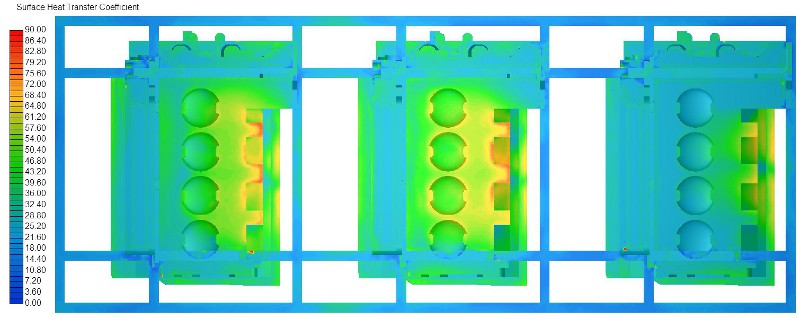
Az irányított öntvény hűtés CFD szimuláció mindent előre megmutat
A fentiek értelmében tehát a CFD szimuláció szolgáltatja a hűtősor paraméterezéséhez és tervezéséhez nélkülözhetetlen adatokat. Attól kezdve, hogy a szimulációk a teljes hűtési folyamatra vonatkozóan elkészültek és az eredmények a rendelkezésünkre állnak, a teljes hűtési folyamat során elvont hőmennyiséget összevetjük a hűtés elején érvényes hőtartalommal. Azonnal kiderül, hogy a tervezett hűtési intenzitás (hűtőlevegő sebesség, a fúvóka pozíciója az öntvényhez képest, az elszívás hatékonysága) elegendő-e a célok megvalósításához.
Ha igen, akkor tovább lehet finomítani a rendszert és növelni annak hatékonyságát. Ha pedig nem, akkor vissza kell térni a tervezési fázis egy korábbi szakaszába és olyan konstrukciót találni, amelyet újra szimulációkkal megvizsgálva már remélhetőleg kedvező eredményt kapunk. Mindezt pedig a számítógép által teremtett virtuális laborban anélkül, hogy a valóságban akár egy szögvasat a másikhoz kellene hegeszteni. Ez a módszer bizonyítottan hatékony és olcsó. Mindenesetre olcsóbb, mint bármit legyártatni, ami aztán nem működik.
Dr. Dúl Róbert
A fenti bejegyzés a Kohászat című lap 147.évfolyam 2014/3. számában a 25-27. oldalon Dr. Dúl Róbert és Dr. Fegyverneki György által jegyzett, Könnyűfém-öntvények hűtési technológiájának tervezése áramlás- és hőtani szimulációval című cikk alapján készült.
